|
|
Вступительный экзамен в ВМШ при ВМК МГУ
имени М. В. Ломоносова
по математике (2003 год)
Задания
вступительного экзамена для 8 класса
1. Решить в неотрицательных целых числах
систему уравнений
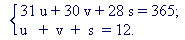
2. Составить с помощью операций
сложения, вычитания, умножения, деления, взятия модуля и с использованием
целых чисел единое выражение
A(x), которое при всяком x  -1
принимает значение 0, при всяком x  0
принимает значение 1, а при всяком x  (-1,0)
принимает значение (x+1).
3. В номере автобусного билета
шесть цифр. Будем называть номер "удачным", если в первой и во
второй тройках количества одинаковых цифр совпадают (например, билеты
075507 и 332323 - "удачные"). Сколько существует различных
"удачных" билетов?
4. Существует ли треугольник, у
которого длина каждой высоты меньше 9, а длина каждой стороны больше 2003?
5. 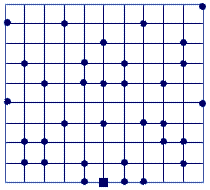 Робот находится в лабиринте из линий (см. рисунок) в позиции,
отмеченной квадратиком, готовый двигаться вверх. Движениями робота
управляет оператор (который робота не видит) при помощи программы,
состоящей из команд следующего вида: символов "Л" (повернуть налево,
оставаясь на месте), символов "П" (повернуть направо, оставаясь
на месте) и натуральных чисел, изображающих число клеток, которые робот
должен пройти последовательно и не меняя направления. Если робот видит
перед собой жирную точку (преграду), то он не может продолжать движение в
том же направлении и начинает выполнять следующую команду программы.
Последний символ программы - не число. Осуществив последний поворот, робот
двигается в заданном направлении, пока это возможно. Если робот, выполняя
программу, побывал на самой верхней линии лабиринта, то в фиксированный
(один и тот же для всех программ с одинаковым числом команд) момент времени
он перешлет оператору сигнал "1", иначе - сигнал "0".
При сборке робота была сделана ошибка, и робот всегда путает повороты.
Написать программу с минимально возможным числом поворотов, которая
обнаруживала бы эту ошибку. Пример: после выполнения программы
"3ППП2Л2П3П3П1Л2Л1П2П1Л", содержащей 12 поворотов, робот перешлет
оператору сигнал "1".
6. Найти все пары целых чисел (x,y),
удовлетворяющих уравнению
41 x4 - 91 y3 = 151.
Задания
вступительного экзамена для 9 класса
1. Составить с помощью операций
сложения, вычитания, умножения, деления, взятия модуля и с использованием
целых чисел единое выражение
A(x), которое при всяком x -1
принимает значение 0, при всяком x 0
принимает значение 1, а при всяком x (-1,0)
принимает значение (x+1).
2. Какому условию должен
удовлетворять радиус r окружности с центром в точке (0;1)
на плоскости Oxy, чтобы данная окружность не имела общих
точек с графиком функции y = x 2 ?
3. Известно, что 1 < a
< 2 и 2 < b < 3. Найти числа c1
и c2 , не зависящие от a и b
и такие, что 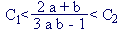 , причем C2
- C1 4.
4. Робот находится в лабиринте из линий (см. рисунок) в позиции,
отмеченной квадратиком, готовый двигаться вверх. Движениями робота
управляет оператор (который робота не видит) при помощи программы,
состоящей из команд следующего вида: символов "Л" (повернуть
налево, оставаясь на месте), символов "П" (повернуть направо,
оставаясь на месте) и натуральных чисел, изображающих число клеток, которые
робот должен пройти последовательно и не меняя направления. Если робот
видит перед собой жирную точку (преграду), то он не может продолжать
движение в том же направлении и начинает выполнять следующую команду
программы. Последний символ программы - не число. Осуществив последний
поворот, робот двигается в заданном направлении, пока это возможно. Если
робот, выполняя программу, побывал на самой верхней линии лабиринта, то в
фиксированный (один и тот же для всех программ с одинаковым числом команд)
момент времени он перешлет оператору сигнал "1", иначе -
сигнал "0". При сборке робота была сделана ошибка, и робот
всегда путает повороты. Написать программу с минимально возможным числом
поворотов, которая обнаруживала бы эту ошибку. Пример: после выполнения
программы "3ППП2Л2П3П3П1Л2Л1П2П1Л", содержащей 12 поворотов,
робот перешлет оператору сигнал "1".
5. Привести пример геометрической
прогрессии {bn} (n N)
такой, что целочисленными элементами в ней являлись бы элементы b7
, b9 , b11 , b13 , b15 и
только они.
6. Найти все пары целых чисел (x,y),
удовлетворяющих уравнению
41 x4 - 91 y3 = 151.
Задания
вступительного экзамена для 10 класса
1. Решить неравенство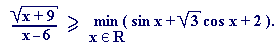 
2. Найти наименьшее a,
при котором уравнение
|x+1| + |x+2| + ... + |x+100| = a
имеет решение.
3. С помощью операций сложения,
вычитания, умножения, деления, взятия модуля и с использованием
действительных чисел задать в виде единой формулы кусочно-заданную функцию
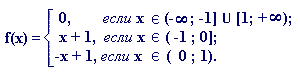
4. Привести пример геометрической
прогрессии {bn} (n N)
такой, что целочисленными элементами в ней являлись бы элементы b7
, b9 , b11 , b13 , b15 и
только они.
5. На какое наибольшее количество
областей могут разрезать плоскость стороны m углов? Ответ
обосновать.
6. Найти все пары целых чисел (x,y),
удовлетворяющих уравнению
41 x4 - 91 y3 = 151.
назад
|
|
